| TOITAの「航空無線通信士受験クラブ」第24期無線工学第10章電気回路 番外編〜枝路の演習問題の解答〜 | |
| 2019年7月4日 9時30分の記事 | |
第10章電気回路 番外編〜枝路の演習問題の解答 今回は、前回掲載出来ませんでした枝路の演習問題 の解答を番外編としてお伝えします。 まずは、問題から見てみましょう。 問題 以下の図のI1からI4とIS の 電流を求めて 下さい。 次にV1とV2の電圧を求めて下さい。 ただし、R1=4 [Ω]、R2=2.6 [Ω]、R3=6 [Ω]、R4=4[Ω]とします。 今回の問題の狙いは、枝電流の理解にあります 。 今回は、無償で全文を公開しています。 [続きを読む]をクリックしてお読み下さい。 当塾は、今年の10月でまる12年になります。 ここまで続けてこられま したのは、皆様方のお陰と感謝して います。 今後も、低価格で分かりやすい合格の為の講座を続けてま いる所存ですので、宜しくお願いいたします。 「時は、金なり」と言いますが、50円を有効に使えていますか ?。 本文には、見本部分の数倍の記事が書いてあります。 2月期の試験は、航空大学校の入学や就職にと大変重要 な試験になります。 独学が難しい事は、特集記事でお話した通りです。 試験迄は、思った程、時間がありません。 時間を無駄にして後悔されない様、本文をお読み下さい。 [お知らせ]有料記事をお読み頂く為には、コンビニで 電子 マネーをお買い求めの上、 下記の URLをクリックしてポイ ントを取得する手続きをお済ませください。 ポイントは、「くる天」様の有料ならではの 他のブログをお 読みになる為にもお使い頂けます。 なお、電子マネー「C-Check」は、2000円 から購入出来ま す。 http://kuruten.jp/blog/help041.html
第10章電気回路 番外編〜枝路の演習問題の解答 今回は、前回掲載出来ませんでした枝路の演習問題 の解答を番外編としてお伝えします。 まずは、問題から見てみましょう。 問題 以下の図のI1からI4とIS の 電流を求めて 下さい。 次にV1とV2の電圧を求めて下さい。 ただし、R1=4 [Ω]、R2=2.6 [Ω]、R3=6 [Ω]、R4=4[Ω]とします。 今回の問題の狙いは、枝電流の理解にあります 。 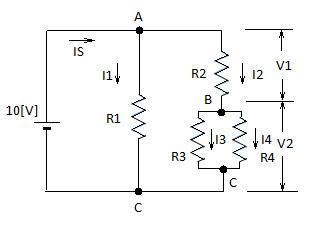 [解答方針] ・R1に流れるI1から求めましょう。 10[V]の電池に4 [Ω]のR1がつながれていま すので、 I1=10[V]/4[Ω] =2.5 「A] ・A→B→Cに流れる電流I2を求めます。 その為には、 R2、R3、R4 からなる合成抵抗 を求めます。 その為には、 R2とB-C 間 (R3とR4の並列接 続) の合成抵抗との直列接続の合成抵抗を RS として 、求めます。 RS= R2 + 1/((1/R3) + (1/R4)) =2.6 [Ω] + 1/((1/6 [Ω]) + (1/4 [Ω])) =2.6 [Ω] + 2.4 [Ω] =5 [Ω] RSは 10[V]の電池に接続されています。 I2 =10[V]/5 [Ω] =2 [A] ついでですからV1も求めておきましょう。 R2 には、I2(2[A])が流れていますので V1=2.6 [Ω] x 2 [A] = 5.2 [V] ・次にI3を求めます。 A-C間の電圧は、電池の電圧です。 V1が5.2[V]ですのでV2は、 V2=10 [V] − 5.2 [V] = 4.8 [V] I3 を求めます。 R3 に掛る電圧は、4.8[V]ですから I3 =4.8 「V]/6 [Ω] = 0.8 [A] ・I4 を求めます。 R4 に掛る電圧も R3に掛る電圧と同じで、4.8 [V] ですから I4 = 4.8 [V]/4 [Ω] = 1.2 [A] I4とI3の電流を足しますと2.0 [A]で I2と同じで す。 つまり、I2 は、それぞれの枝路であるR3 と R4 に分かれて流れた事になります。R3とR4 に分か れた電流は、右側のC点で合流して I2となります 。 ・IS を求めます。 IS は、A点でI1とI2に分かれていますので IS = I1 + I2 = 2.5 [A] + 2 [A] = 4.5 [A] 左側のC点で I1とI2 が合流してISになります 。 問題には、有りませんが、A-C 間の 4つの抵抗 の合成抵抗値で電池の電圧を割ってみて下さい。 IS = 4.5 [A] になるでしょうか? 計算してみて下さい。 [解答] I1=2.5[A]、I2=2[A]、I3=0.8[A]、 I4=1.2[A]、IS=4.5[A]、V1=5.2[V]、 V2=4.8[V] [枝路に流れる電流の求め方のまとめ] 1.幾つかの並列のカタマリに分けます。 この問題でしたらR1 を 1 つのカタマリとして そ の他 をもう1つのカタマリとします。 2.それぞれのカタマリの合成抵抗を求めます。 3.それぞれの合成抵抗値で電源電圧を割る事で それ ぞれのカタマリ (枝路) に流れる電流を求めます。 4.それぞれの枝路を さらに直列のカタマリに分けま す。この問題でしたら、R2 とそれ以外の2つの抵 抗R3とR4から成るカタマリです。 5.それぞれのカタマリ(並列または、1 つ)の 合成抵 抗を求めます。 6.それぞれの合成抵抗に”3”で求めた電流をかけます 。 これで、”4” の直列のカタマリのそれぞれの電 圧が求まります。 7. ”6” で求めたそれぞれの電圧を それぞれの直列回 路を構成する並列接続された各抵抗で割りますと 直列に分けた並列接続された抵抗 1つ 1つに流れ る電流が求まります。 [枝路の重要ポイント] 電池(電源) から流れる電流は、途中でそれぞれの枝 路に分かれても、 枝路を出た電流は、電池に戻る所 で合流し、 電池から流れ出た電流と同じ量の電流と なって電池に戻ります。 今回は、 電気回路の基礎である抵抗で枝路を考えま したが リアクタンスで構成される直並列回路につい ても同じです。 次回は、RLC並列回路のお話を致します。 | |
| このブログへのチップ 0pts. [チップとは] [このブログのチップを見る] [チップをあげる] |
| このブログの評価 評価はまだありません。 [このブログの評価を見る] [この記事を評価する] |
|
◆この記事へのコメント | |
| コメントはありません。 | |
|
◆この記事へのトラックバック | |
|
トラックバックはありません。 トラックバックURL https://kuruten.jp/blog/tb/toita_1day/429829 |
|


