| TOITAの「航空無線通信士受験クラブ」第22期無線工学第10章電気回路 (6)電力その1 | |
| [無線工学] | |
| 2018年6月29日 9時30分の記事 | |
第9章電気回路 (5)電力その1 最近、 大学の電気関連の学部においても、力率を扱わ ないケースが有る様です。 扱わない理由は、色々有ると思いますが、力率は、 難 しいものと思われいる節があります。 航空無線通信士 の試験を受験される方は、 試験に出ると言う事もあり ますが、 簡単ですので、今回のお話を通じて理解して おいて下さい。 そして、超簡単に 三角関数が理解出来る方法をお話い たします。 1.電力とは? 続きは、[続きを読む]をクリックしてお読み下さい。 今回は、全文無償で公開しています。 当塾は、昨年の10月でまる10年になりました。 ここまで続けてこられま したのは、皆様方のお陰と感謝して います。 今後も、低価格で分かりやすい合格の為の講座を続けてま いる所存ですので、宜しくお願いいたします。 「時は、金なり」と言いますが、50円を有効に使えていますか ?。 この資格は、皆様にとって取れれば、リターンの多い資格 です。 試験迄の時間を無駄にしない様にして下さい。 [お知らせ]有料記事をお読み頂く為には、コンビニで 電子 マネーをお買い求めの上、 下記の URLをクリックしてポイ ントを取得する手続きをお済ませください。 ポイントは、「くる天」様の有料ならではの 他のブログをお 読みになる為にもお使い頂けます。 なお、電子マネー「C-Check」は、2000円 から購入出来ま す。 http://kuruten.jp/blog/help041.html
第9章電気回路 (5)電力その1 最近、 大学の電気関連の学部においても、力率を扱わ ないケースが有る様です。 扱わない理由は、色々有ると思いますが、力率は、 難 しいものと思われいる節があります。 航空無線通信士 の試験を受験される方は、 試験に出ると言う事もあり ますが、 簡単ですので、今回のお話を通じて理解して おいて下さい。 そして、超簡単に 三角関数が理解出来る方法をお話い たします。 1.電力とは? 電力とは? と質問しますと皆様は、以下の様に答 えられると思います。 P(:電力)= V(:電圧) x 電流(:I)(1) 直流の場合は (1)式で良いのですが、前回迄のお 話の様にコイルやコンデンサーが回路内にありま すと電流と電圧の間に位相差が生じてしまいます。 その位相差を考慮しますと (1) 式は、(2) 式の様 になります。 P = V・I・cosθ (2) ここで θ は、 電圧と電流の位相差です。 そして cosθ を力率と言います。 何故、cosθを電流と電圧の積に掛けるのでしょう か? 下の図をご覧下さい。 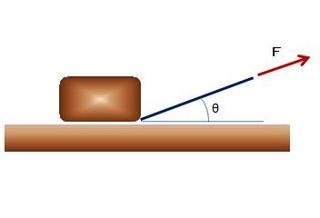 荷物を右側へ引っ張る様子を描いています。 物理の世界では、 荷物を水平移動する事を「仕 事」と言います。 仕事を W とし、 水平に動かした距離を L とし ますと W = F・L (3) となります。 F は、力です。 上の図で θ が ”0°”つまり、地面と水平に力を 加えれば良いのですが、図の場合、 θ が ”0°” では、ありません。 それでは、 θ が ”0°" でない時の 仕事は、どの 様に考えれば良いでしょうか? θ が "0°” でない時、 力:F がどれだけ 水平方 向へ引っ張る事に寄与するかを 考えてみたらど うでしょうか? 図の F をベクトルと考えますと Fの水平面への 影が、横方向へ動かす力となります。 と言う事は、横方向への力を Fh としますと Fh = F・cosθ (4) となります。つまり、F に cosθを掛ける事によ り F の水平方向の成分(有効成分)を求めた事 になります。 よって(3)式の一般式は、 W = F ・cosθ・L = F ・L・cosθ (5) となります。 θ= 0°で F は、全て (100%)有効になります。 θ=90°では、F は、0%が有効と言う事になり ます。 横 (水平) 方向への移動が仕事ですのでθ=90° と言う事は、垂直に持ち上げる事ですので 水平 方向への移動は、有りませんので仕事は、”0”で すネ。 次に(5)式 のcosθ を sinθで考えてみたらどう でしょうか? その前に sin と cos についてのおまけです。 sinやcosについて忘れてしまった方もいるかも 知れませんネ。 忘れる理由は、理解出来てないからです。これ は皆様が悪いのでは、なく、教えかに問題があ るのです。三角形の辺の呼び方は、時代による 様です。 ”斜辺”、”高さ”、”底辺”とか私の頃は、”高さ” を”隣辺”と言ったと思います。 簡単な三角形なら良いのですが、三角形によっ ては、どこが”底辺”だかどこが”斜辺”だかが分 からなくなってしまいます。そして sinやcos、 tan の覚え方を教わったところで所詮、記憶に たよる為に、時間と共に忘れてしまうのは、当 然の事です。 それでは今日から三角関数を超簡単に理解して 一生ものの知識にしましょう。一生、忘れませ んヨ。 {三角関数⇒円関数] 三角関数って分かりずらいですね。 角度が90度迄の範囲は良いのですが、sin135° って幾つになるのでしょうか?」と聞かれて直 ぐに答えが出ますか? 先に述べましたが、何処が斜辺で、何処が高さ か分からなくなるからです。 それでは、超簡単に理解する方法をお話致しま す。 図-1をご覧下さい。 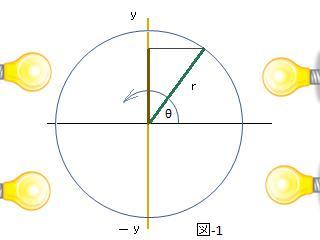 y軸とx軸 (図では、真ん中の横線です。) と の交点を支点として長さ:r の棒が廻ってい ます。 y軸の左右に電球を置き棒を照らします。 すると、棒の影が y軸上 (図では、茶色の太い 線で表しています。) に出来ます。 この影の長さが sinθの値です。 135° でしたら、90° と180° の間ですので、 棒は、左上(第2象限) にいます。棒の影は y 軸の+側に出来ます。 影の高さは、(225°− 180°) = 45°の場合と 同じです。 sin45°= 1/sqrt(2) です。 そして、 棒は、左上(第2象限)にいますので sin135°=1/sqrt(2) となります。 それでは、sin315°は、いかがでしょうか? 棒は、右下 (第4象限) へ来ていますので、 (315°− 270°)= 45° で考えれば良さそう です。 sin45°= 1/sqrt(2) です。 そして、影は x軸より下ですので ”−” です。 sin315°= −1/sqrt(2) となります。 sinθは y軸への影 と考えれば、何処が斜辺 だとか高さだとか考える必要がありません。 次にcosθを考えます。 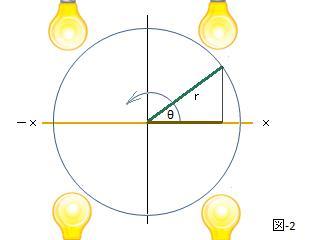 cosθは、x軸への棒の影です。 cos225°は、−1/sqrt(2)。cos315°は、 1/sqrt(2) になる事を確認しておいて下さい。 以上、お話いたしました通り、三角関数は、円 関数 と考えれば良いのです。 ※sqrtは、平方根を表します。sqrt(2) =1.414 になります。 sin は、只今お話をしました様に棒に垂直面へ の影 (棒の先端の高さ)になりますの無効を表し ます。 (5)式の cosθ を sin θ にしますと仕事には、 寄与しなかった無効の仕事量を求める事になり ます。 実は、 電力は、 仕事率の事なのです。仕事率 とは、時間当たりどれだけの仕事をしたかを表 します。 電圧の単位は、[V] ですが、[V] は、[J/C] の 事です。 そして、 電流の単位である [A] は、[C/S] の 事です。 [J/C] とは、1 [C] の電荷当たりの仕事量の事 です 。 そして [C/S] とは 1秒間当たりの 電荷の変化 量 (移動する電荷の量) ですので、 電圧と電流 を掛けますと その単位は、 [J/C] x [C/S] = [J/S] となります。つまり、1秒間当たりの仕事量で す。1 秒間当たりの仕事量とは、仕事率の事で す。 単位から電力は、電圧と電流を掛けたもので仕 事率を求めていた事がお分かりになったと思い ます。 交流の場合、電流と電圧の積に 力率を掛けま すと 仕事率の 有効な部分を求める事が出来ま す。 この時の θ は、位相差の事です。 回路に抵抗しかない時は 抵抗に流れる電流と 抵抗の両端間の電圧との位相差が ”0°”ですの で、一番効率が良い事になります。 力率の単位は cosθの値に100を掛けた [%] です。 θ = 0 なら力率は、100 [%] と言います。 次回は、” 3 種類の電力”と”力率の改善”についてお 話をいたします。 | |
| このブログへのチップ 0pts. [チップとは] [このブログのチップを見る] [チップをあげる] |
| このブログの評価 評価はまだありません。 [このブログの評価を見る] [この記事を評価する] |
|
◆この記事へのコメント | |
| コメントはありません。 | |
|
◆この記事へのトラックバック | |
|
トラックバックはありません。 トラックバックURL https://kuruten.jp/blog/tb/toita_1day/411090 |
|


